A truncated tetrahedron is an Archimedean solid, created by slicing a tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a tetrahedron, first join its faces to create a closed polysurface. Now, you may recreate the lines of the tetrahedron’s edges, either by drawing them or generating them (Curve / Curve from Objects / Duplicate Edge). While the edge lines are selected, hit (Curve / Point Object / Divide Curve / Number of Segments) and type 3 to create the number of segments. Now, all edges should be divided equally into three parts. Draw the equilateral triangles, connecting the division points. Trim the tetrahedron (polysurface) using these triangles. And triangular cap holes (Solid / Cap Planar Holes) to finish the Archimedean Solid of the truncated tetrahedron. Below is a step-by-step explanation of this process in Rhino. You can follow it after modeling a regular tetrahedron.

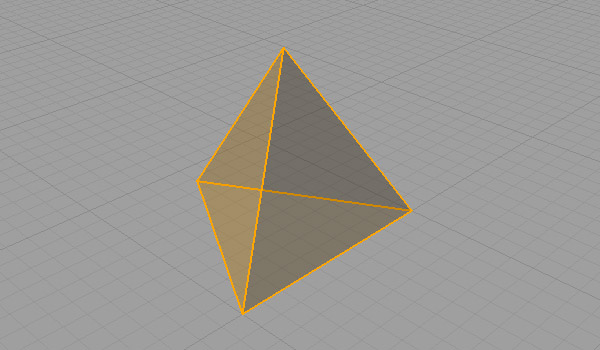
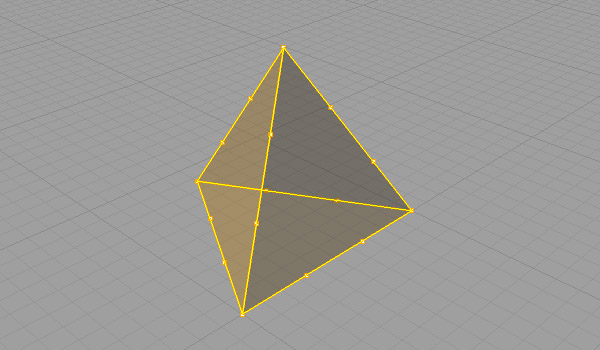
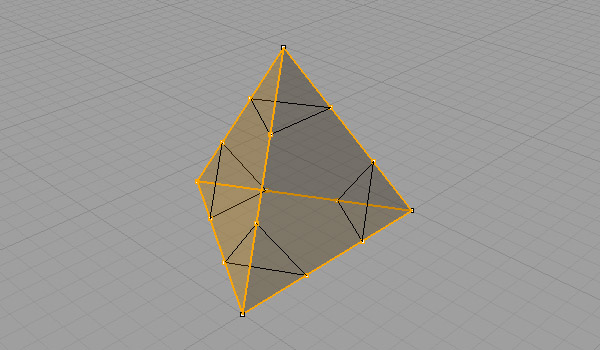
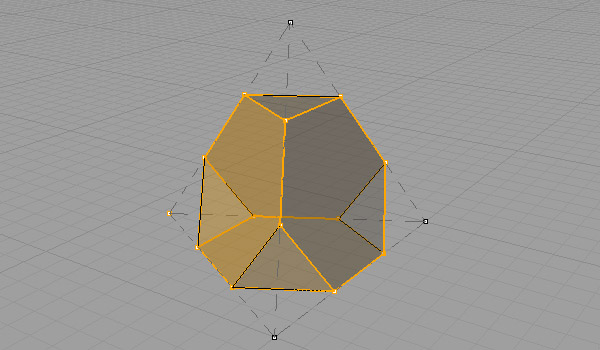
The truncated tetrahedron has the same symmetry group as the regular tetrahedron, which is the tetrahedral group. This one is the basic exercise for the truncation operation in polyhedra geometry. Its dual is the Catalan solid, Triakis Tetrahedron. Maybe I should be modeling that one in the future. However, it looks possible to write code about the dual polyhedra.

We also examined the truncated tetrahedron in more detail in the video here. If you want to support this website by downloading my files, would you consider being my Patreon? The link to my Patreon page includes the working Grasshopper and Rhino files for many projects. Thank you.