Vector Arithmetics in Rhino Python
Today, I am going to advance the Vector class a bit more. Firstly, I will improve the display method I introduced recently. Then, I will add two new methods which handle the fundamental vector arithmetics in Rhino Python.
Improving the Display Method
In the previous attempt, I displayed vectors on the origin of the Rhino viewport. The coordinates of the tail of a vector are not stored within the object attributes. Normally, I can store two coordinates, one for the tail, one for the tip. That seems logical. But in the future, we are going to see that, the actual length of the vector (the amounts of displacement in x, y, and z) will be the core elements of many calculations. This is why I stored only the tip point information. However, while displaying vectors, an origin point can be used. I am adding this optional functionality in the below code:
def display(self, origin=[0,0,0]):
v = self.components
tip = [v[0]+origin[0], v[1]+origin[1], v[2]+origin[2]]
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)| Line | Explanation |
| 1 | Start the definition of the “display” method. This time, the method will take one optional input. This input, “origin” is an optional one, with a default value of [0,0,0]. |
| 2 | This time, I am assigning self.components in a new, temporary variable named “v”. Because I am going to use self.components several times. This makes those lines shorter. |
| 3 | We define “tip” as a new variable. This variable is a list of three elements (square brackets and elements are separated by a comma). Each element of this list is an addition of the components of the vector, and the elements of the origin (which is another list of three numbers). |
| 4 | A new variable named “line” is defined. This is the line drawn by rhinoscriptsyntax’s AddLine method. The line is drawn from the optional origin point to the tipping point calculated in the above line. |
| 5 | Create an arrowhead on the line created in the above line. |
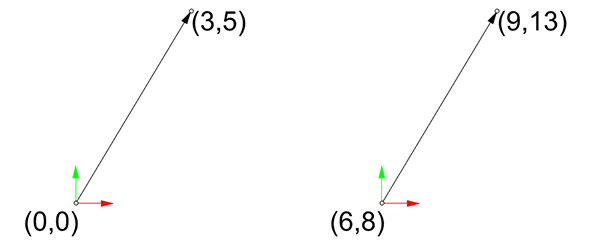
The below figure shows the calculation of the vector’s tip point according to the varying origin.
Vector Arithmetics: Vector Addition Method
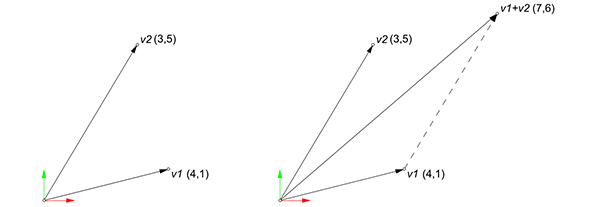
This method will take two vectors, and output their summation as a new vector. This is one of the fundamental operations we will be using in the future. The below figure explains the vector addition procedure. Thus, it is adding one vector’s tail to the other’s tipping point. Basically, it is the addition of the x, y, and z components of the two vectors.
def add(vA, vB):
v1 = vA.components
v2 = vB.components
addition = [v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2]]
return Vector(addition)| Line | Explanation |
| 1 | Start the definition of the “add” method of the Vector class. Here, the method will take two vector objects as inputs. Notice that the method does not take “self” as an input. This makes the add method a “class method”. We are going to call this method, not from an object, (such as object.add()) but from the name of the whole class (Vector.add()). |
| 2 | A temporary variable v1 is defined, taking the components of the first input vector. |
| 3 | A temporary variable v2 is defined, taking the components of the second input vector. |
| 4 | A new variable named “addition” is defined as a list of three numbers. Therefore, each element of this list includes the addition the corresponding elements from v1 and v2. |
| 5 | The return statement in Python determines which object or data will be transferred to the code that fires this method. For example, the AddLine method in rs returns the ID number of the line object. |
Vector Arithmetics: Vector-Scalar Multiplication Method
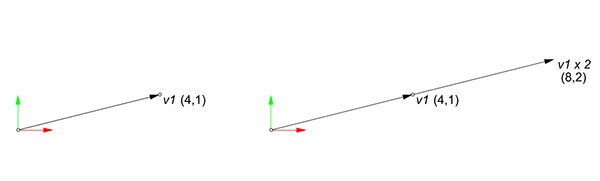
We will need another important operation: vector-scalar multiplication. When we multiply a vector with a scalar (number), we multiply the components of the vector (coordinates, in our case) by that number. As you can see, the below figure explains this.
def multiply(self, s):
v = self.components
return Vector([v[0]*s, v[1]*s, v[2]*s])| Line | Explanation |
| 1 | Start the definition of the “multiply” method. The method takes one input, s, a number to be multiplied with the vector (self). |
| 2 | Define a temporary variable, “v” that keeps the components attribute of the vector. |
| 3 | Return a new vector object (notice the Vector() constructor) by giving a list of three numbers as an input. This input is calculated by multiplying each coordinate by the s. |
Conclusion: Vector Arithmetics
Today, I started studying vector arithmetics and developed new methods for it. Below is the latest code I have been coding since the beginning.
import rhinoscriptsyntax as rs
class Vector:
def __init__(self, point):
self.components = point
def display(self, origin=[0,0,0]):
v = self.components
tip = [v[0]+origin[0], v[1]+origin[1], v[2]+origin[2]]
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)
def add(vA, vB):
v1 = vA.components
v2 = vB.components
addition = [v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2]]
return Vector(addition)
def multiply(self, s):
v = self.components
return Vector([v[0]*s, v[1]*s, v[2]*s])Now, we can test the above code by creating new vector objects and doing arithmetic operations with them.
myvector1 = Vector([3,5,0])
myvector2 = Vector([4,1,0])
myvector3 = Vector.add(myvector1, myvector2)
myvector1.display([5,5,0])
myvector2.display([5,5,0])
myvector3.display([5,5,0])