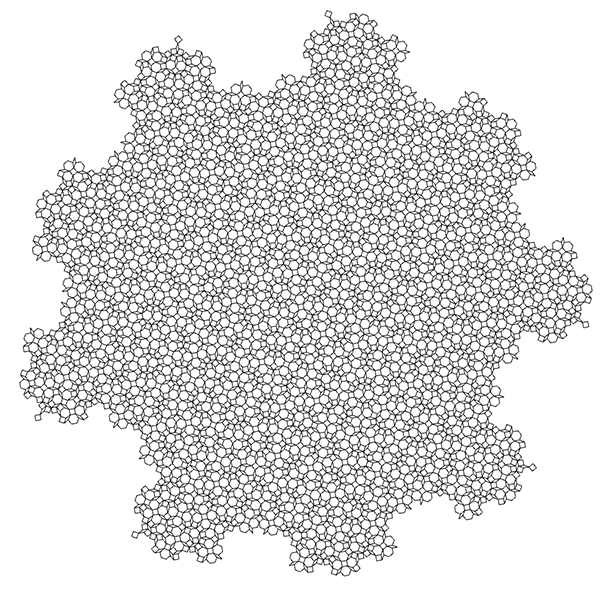
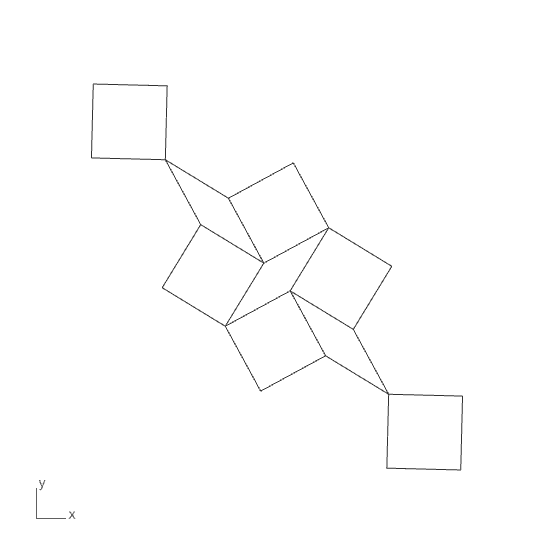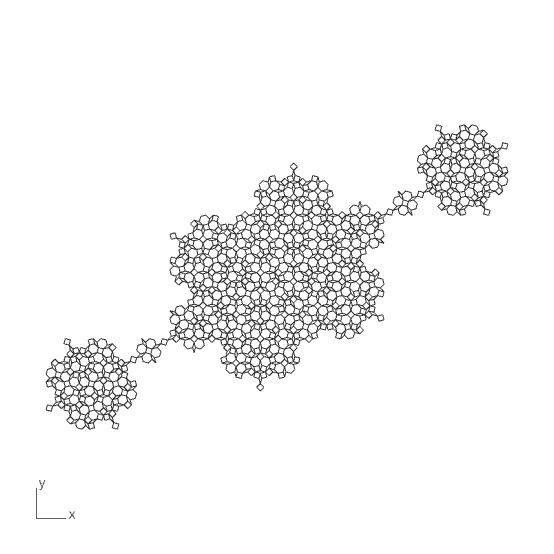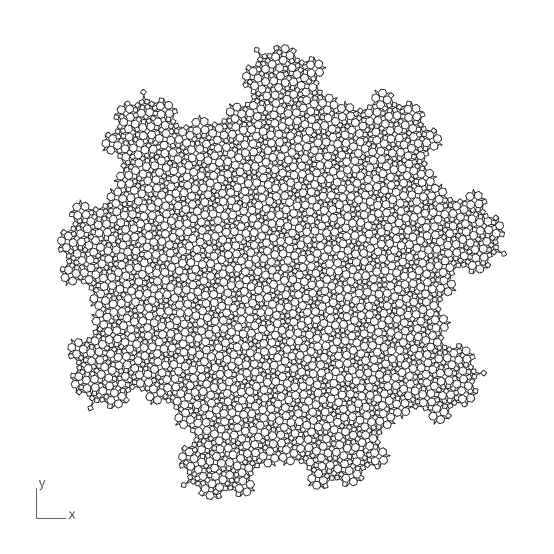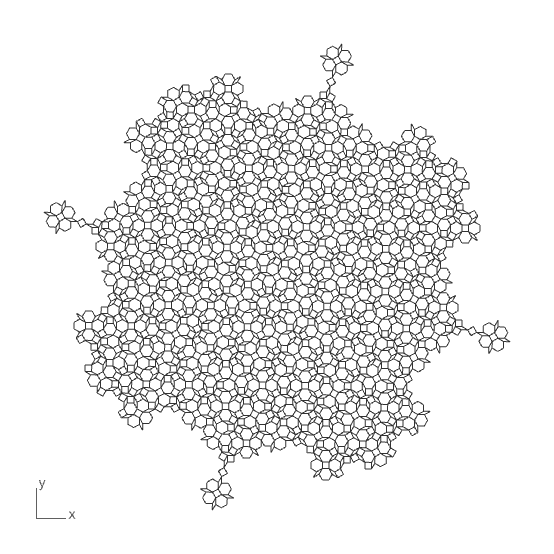
Socolar Tiling
An aperiodic tiling is a pattern that covers the plane without ever repeating itself (i.e., it is non-periodic). A few special shapes, arranged according to specific rules, can cover the entire plane, but the resulting pattern never repeats exactly. I challenged myself on a 3-day coding sprint to create a general-purpose script in Grasshopper that could generate these tilings. I set Socolar Tiling as my first target. This link contains great information about this and many other aperiodic tilings. Socolar Tiling has three substitution rules with squares, hexagons, and rhombuses.
My first objective was to enable Grasshopper to recognize a specific set of 2D shapes. I developed a cluster that explodes incoming shapes, calculates the distances of their vertices from the shape’s centroid, sums these distances, and then normalizes them by dividing by the longest distance. This method turned out to be useful. For instance, a shape now returns a “fingerprint value” of 1.1666 for a hexagon, 1.25 for a square, and 0.883975 for a rhombus, regardless of scale. It was not possible to determine this only by counting the number of edges, since the square and rhombus have the same number of edges. Then, the next step is to use it as a base and draw the tiles of Socolar Tiling. The challenge was ensuring the new shapes are placed correctly, even when they vary in scale and angle. I placed the vertices of the new shapes using polar coordinates relative to the plane of the source shape. 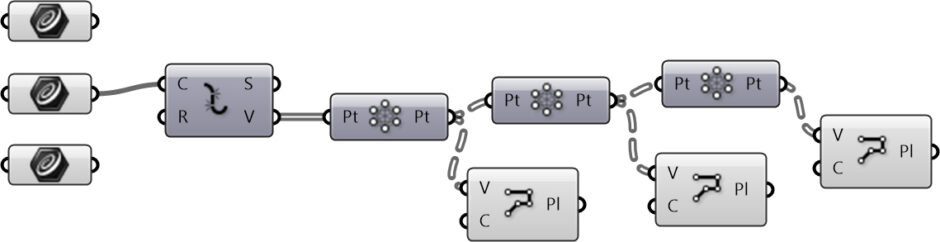I created the final product as a cluster. So that you can chain them together to generate multiple iterations of the tiling. I recommend you check the “fingerprint” clusters there. It is the interesting part, I guess.
Cite this post
Related Posts
Penrose Tiling Generator
April 16, 2024
A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created a simple Penrose Tiling Generator in Grasshopper. I used the…
Scary Patterns
August 6, 2026
While digging through my archives, I found an old animation I made in 2023. Back then, I was generating patterns with Parakeet. Thanks to this talented add-on, I managed to create a nice pattern by dressing a different component onto a Snub Square tiling base. However, for some reason, things started turning into a horror movie after that. MultiPipe was popular back then. So, I converted this pattern into surfaces using MultiPipe and attempted an animation using Rhino’s rendered viewport…
Evolutionary Optimization of Tilings
April 19, 2025
In large-scale projects, calculating tiling layouts for wall, floor, and ceiling surfaces becomes even more critical. Evolutionary optimization of these tilings seemed to be a viable approach yesterday. Considering how time-consuming and labor-intensive this process can be, I tried using Galapagos, an old but often overlooked feature in Grasshopper, which might be particularly useful in this situation. Galapagos provides an alternative interface for evolutionary optimization within Grasshopper. It works by minimizing or maximizing a fitness value you define, using parameters…
Hexagonal Star Lattice
December 18, 2023
Here are the variations of classical six-pointed star patterns generated by Grasshopper. Generally, you can see these patterns under the title “Islamic patterns” because they are frequent in the decorations of mosques and palaces. I studied these patterns in Grasshopper earlier in these posts. I always find this an interesting geometry exercise. This time, my main goal was to develop a useful code only with the native Grasshopper components that create laser-cut-ready products of hexagonal star lattice. Thus, I made…
Star Lattice
May 15, 2023
This is the six-pointed star lattice definition in Grasshopper. The definition is generating CNC or laser-ready results as seen below. In this code, first, I developed a common star pattern by exploding a hexagonal grid. The tricky part of this definition is the last part. There, you can see how you can use the Region Union (RUnion) component to add thickness to a pattern we have drawn before. The operation here will require trimming and extending commands under normal conditions….