[2011_12_25_divide] here is the fundamental of surface subdivision in Grasshopper. In order to design a parametric truss exercise, this is the generally accepted starting point. Get a surface from the file, subdivide it into U and V directions to create point lists, and then manipulate these points to create something interesting. Having a list of points would also present good potential regarding attraction with other entities, such as point or […]
NURBS surfaces by nature, like four-corner topologies with U and V directions. Şebnem Yalınay Çinici has formulated a tectonic exercise of “Primitive Hut”, which in my point of view is a tough geometric challenge; a subdivision on a real three-corner manifold. That seems very easy at the beginning as both Rhinoceros and Grasshopper are able to create surfaces with three corners, by either lofting, meshing, or edge curve methods. However, those […]
This experiment is based on a traditional surface-component definition. However, the variation of components is associated with Gaussian curvature. We just control the subdivision and a multiplier value. Results are interesting in as an educational tool to explain NURBS surface curvature and its utilization for Design Geometry. Different surface shapes generate exciting results. Of course, this could be much improved by recognizing positive and negative curvature values, (probably only accepting […]
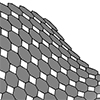
Back in 2011, one of the first posts on designcoding explored how to divide a surface in alternative ways. I called this Grasshopper definition a semi-regular surface tessellation. Although the term isn’t entirely accurate -since the pattern is neither planar nor made of equilateral shapes- it still reflects what I had in mind. Dividing surfaces into fabricable parts remains a key concept in learning parametric modeling, so I decided to […]
