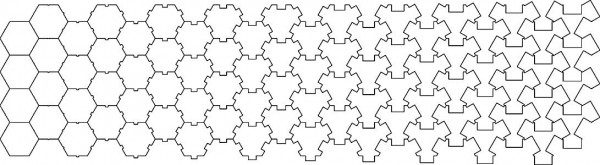
Trifoliolate
The Parquet Deformation exercise is generally originated with William Huff. Huff conducted it at several schools of architecture since the 1960s. Huff defines the exercise as rooted in two analytical disciplines; monohedral tilings in geometry, and the continuous deformations in biological morphology. This is generally exemplified by D’Arcy Thompson’s and Albrecht Dürer’s studies. One of the student’s works of Huff, Trifoliolate is a single-axis, single-prototile hexagonal parquet deformation. It was designed by Glen Paris at the studio of William Huff in 1966. I tried to analyze it and reconstruct it in several different ways. The Grasshopper code was surprisingly simple. Here is the result:

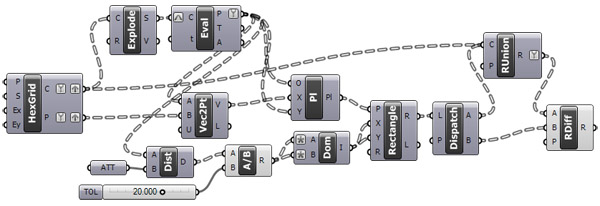
Here is a small phrase from Douglas Hofstadter:
Three of my favorites are “Crazy Cogs”, “Trifoliolate”,and “Arabesque”. They all share the feature of getting more and more intricate as you move rightward. Most of the earlier ones we’ve seen don’t have this extreme quality of irreversibility-that is, theratcheted quality that signals that an evolutionary process is taking place. Is there any way you can back out of that super-tangle except by retrograde motion-that is, retracing your steps? I suspect there is, but I wouldn’t care to try to discover it.
Hofstadter, D., 1983, “Metamagical Themas Questing for the Essence of Mind and Pattern”, Chapter 10.
When you switch the x and y axes of the plane, strange patterns start to emerge:
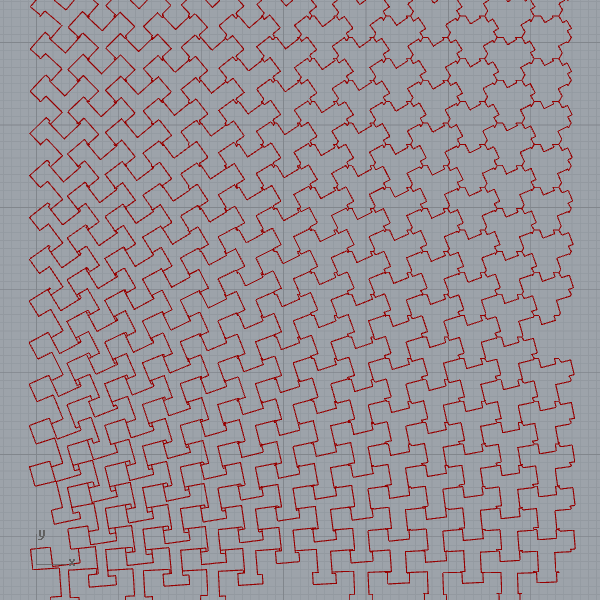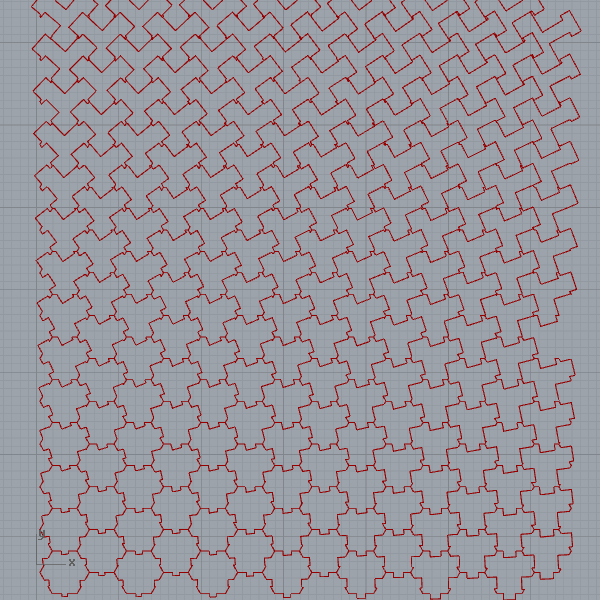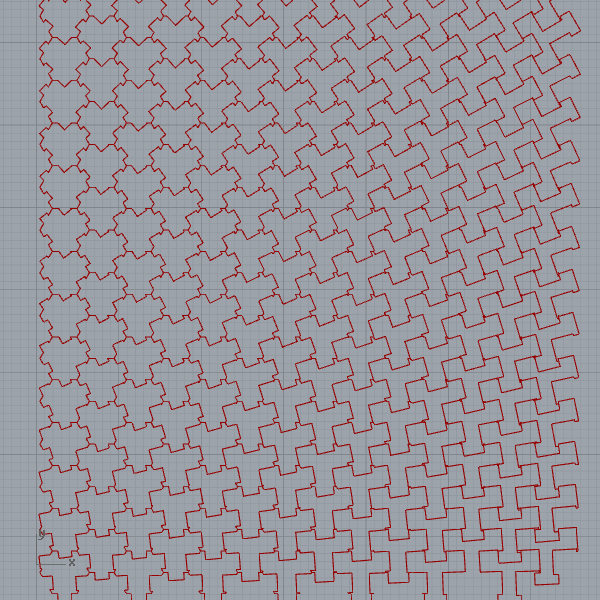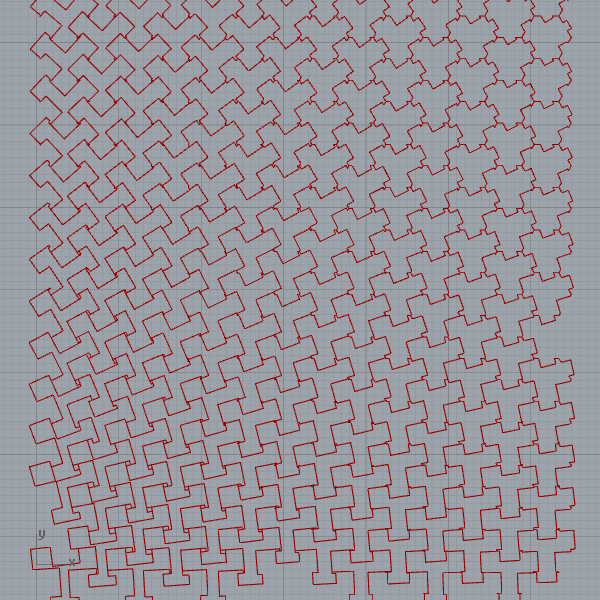
I love the contrast between the simplicity of the code and the rich variations it produces. Here is a journal paper I wrote about parquet deformations. In the paper, there are three reconstructions of classical parquet deformations with Grasshopper. I developed the below definition in 2013. But it still works without any problem in 2021.