#aperiodic

An aperiodic tiling is a pattern that covers the plane without ever repeating itself (i.e., it is non-periodic). A few special shapes, arranged according to specific rules, can cover the entire plane, but the resulting pattern never repeats exactly. I challenged myself on a 3-day coding sprint to create a general-purpose script in Grasshopper that could generate these tilings. I set Socolar Tiling as my first target. This link contains great information about this and many other aperiodic tilings. Socolar…

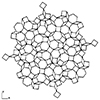
A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created a simple Penrose Tiling Generator in Grasshopper. I used the…