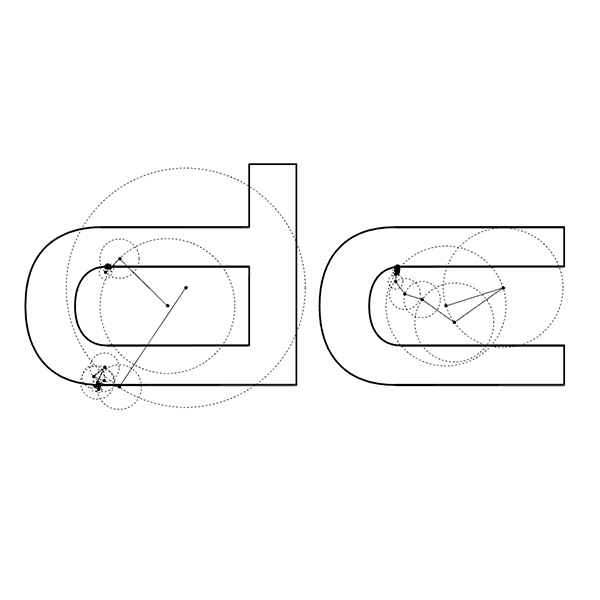
Discrete Fourier Transform
The Fourier Transform is a powerful mathematical technique that allows us to analyze the different frequency components within a signal or shape. Its discrete version, the Discrete Fourier Transform (DFT), is used when working with numerical data. I studied the Fourier Series here before. One of the most fascinating aspects of the DFT is that it can represent a signal or shape using rotating circles (or vectors). Each circle corresponds to a specific frequency, amplitude, and phase. When connected in sequence, these circles collectively recreate the original shape over time. With this approach, we can reconstruct even a complex curve using simple harmonic motion.
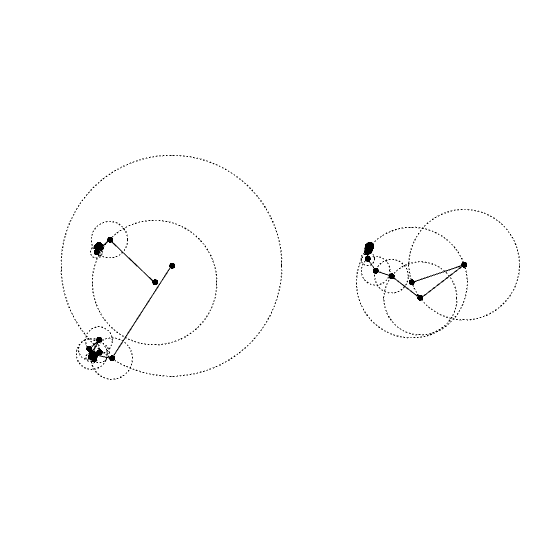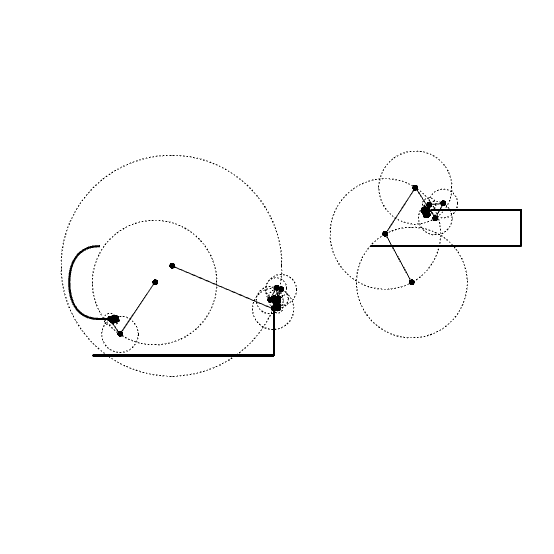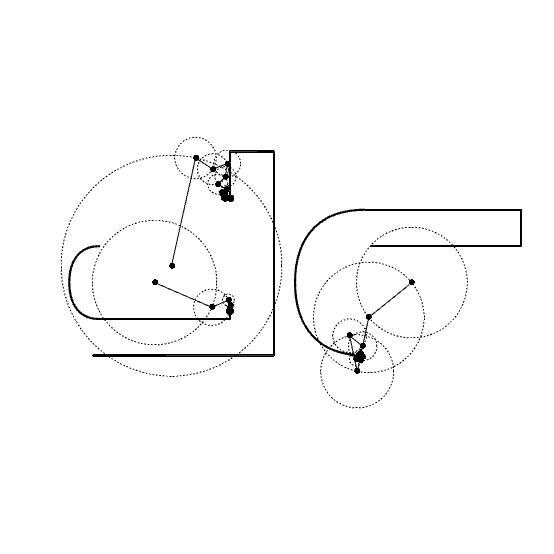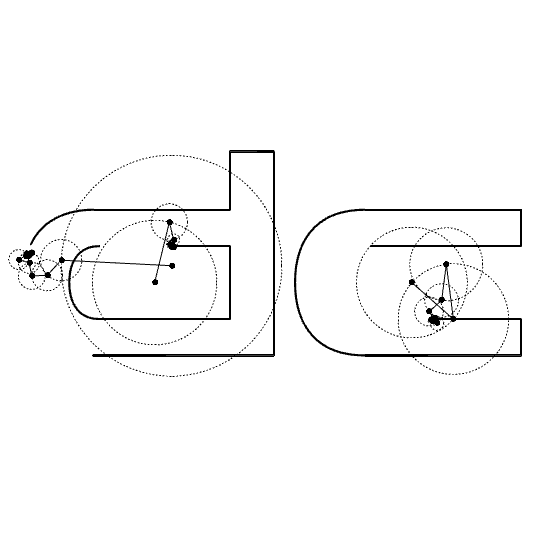
For example, consider a closed curve—perhaps hand-drawn. If we sample this curve into a list of points and represent each as a complex number (like x + iy), we can apply the DFT to extract the frequency components. 3Blue1Brown, Mathologer, and the Coding Train have informative videos on the math behind this. The result is a series of rotating vectors, each spinning at a specific rate. The tips of these vectors trace out the original shape as time progresses. Discrete Fourier Transform animations are both visually striking and deeply intuitive. They make it easier to understand how Fourier analysis works beneath the surface. In visual programming environments like Grasshopper, experimenting with DFT opens up a world of artistic and educational possibilities. It transforms mathematics into a drawing tool, turning abstract theory into something we can see and feel.
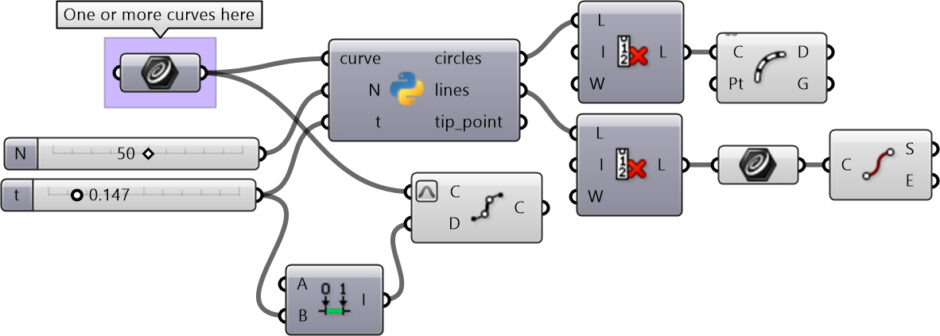

Above is the Grasshopper definition and the Python code that calculates the rotating circles. If you liked this content and want to support me, you can be one of my patrons here and download my working Grasshopper file on the Discrete Fourier Transform.