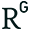Today’s fractal is the Julia Set, the amazing simplicity of chaos. There are lots of applets and articles on the internet about this fractal. You can generate this with the iteration of a basic function many times and placing points on the complex plane. I developed a Grasshopper implementation in 2012. Also, this was my first study on complex numbers. At each iteration, the detail level increases. I utilized a common brute-force approach, distributing a grid of points, converting them to complex numbers, using the expression (usually in the z² + c form, where c is a constant complex number and z is the variable one). Then check the modulus of the resulting complex number against a value (usually 2 or 3). I used a VB.net component to calculate the expression. Python was very slow compared to VB.net.

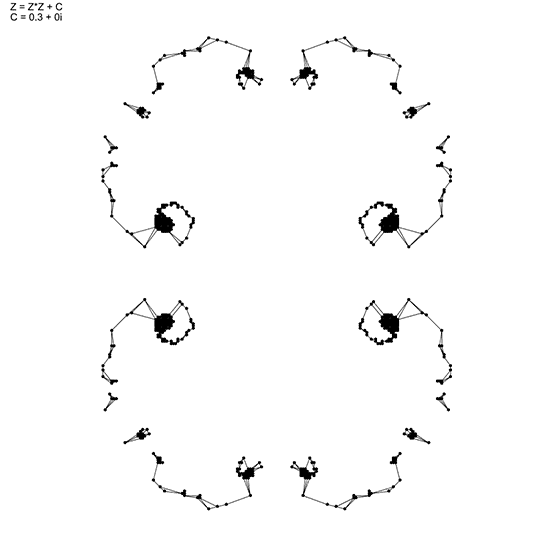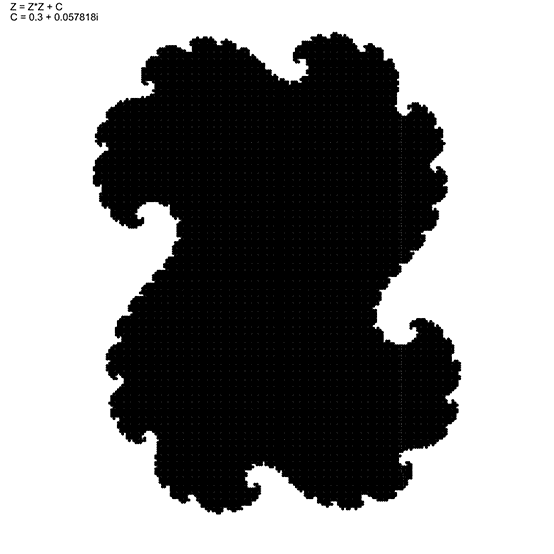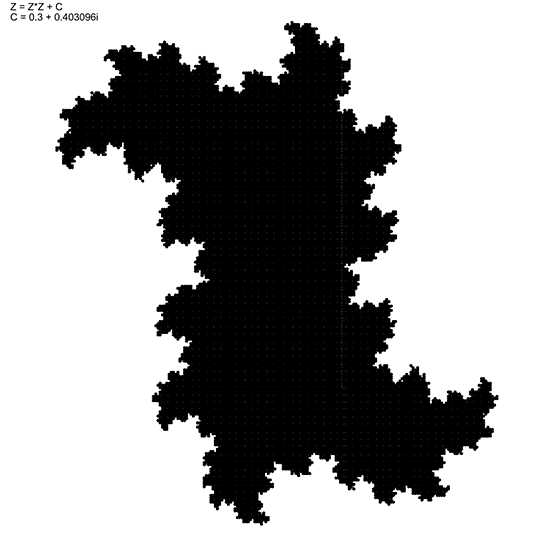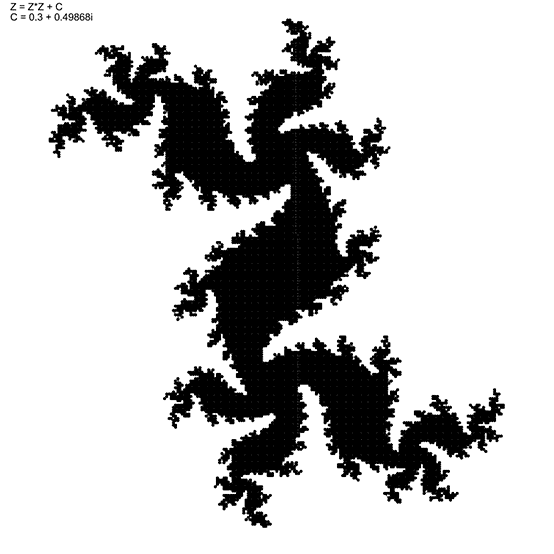
This Grasshopper definition generates the Julia Set fractals with several input parameters. The user can modify the number of iterations, c and d variables, and also the formula itself. You can generate the infinite possibilities of Julia Set. The outputs are point objects. The code does not generate boundary surfaces or curves. I made the definition with the help of native Grasshopper components and a VB.net code. So, you don’t need to install external add-ons to be able to use the definition.

You can re-build the definition by looking at the image above. However, you need to code the VB.net script that iterates the formula and spits out a number. Please be careful when opening the definition, they can exhaust your CPU. If you liked this content and want to download and use my code, would you consider being one of my Patreons? Thank you.