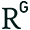Defective Use of Algorithms: TPI Disability
This is based on my failure of creating an optimum solution for planar polygonal subdivisions. There is a method called Tangent Plane Intersection (TPI), explained briefly here (sometimes similar algorithms are called “planar remeshing” and “variational shape approximation”) which is effectively used in the Trada pavilion (here). I tried to implement a similar method using only native Grasshopper components and no recursion, but it quickly became much more complicated than I thought. It was based on the simple idea that I can obtain the tangent plane of any point on a surface. By expanding circular planar surfaces on these planes, multiple planes intersect and create a planar polygonal subdivision eventually. However, there are some cases (some angular intersections) where this logic does not work properly and has to be edited. I quit at this stage but saw that it became an interesting definition by itself. This is why I called this post a disability. It is caused by the fact that Grasshopper it very hard to handle multiple events at the same time. I couldn’t tell Grasshopper that it should treat multiple plane intersections together in a fashion that would create the smallest surface areas. Of course, there are lots of different approaches and solutions to this problem. Maybe I can return and continue this research further. Anne Bagger calls her system a “plate shell”, and you can check her works here. Also here, here, you’ll see some other research on this topic.
The definition below is logical but not functional. It uses Delaunay connectivity to check the adjacent points, then attempts to calculate the growing amount of isovist ranges to create the edges of planar surfaces. What an epic fail it is. Here is the Grasshopper definition: [GHX: 0.9.0056], you should manually input a surface to it;
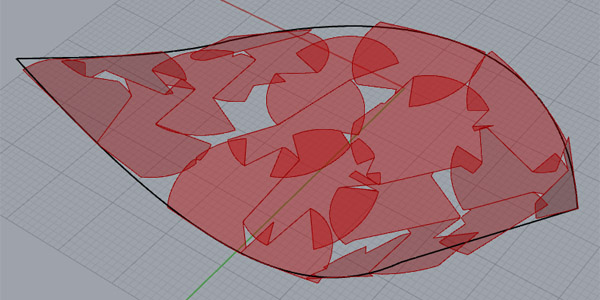
An optimization system might allow diverse design paths to emerge when it fails. This might be one of the points that designing is not an optimization. It is somehow a reflective optimization of personal stimulations, but of course, includes much more than that.