Approximating Gyroid
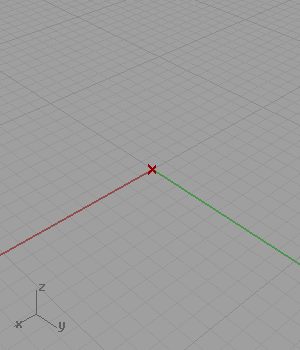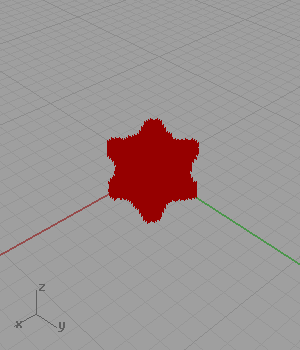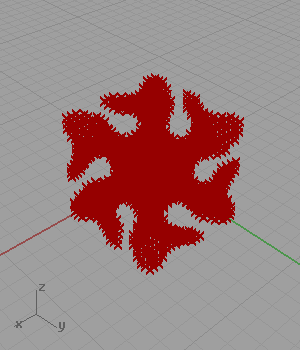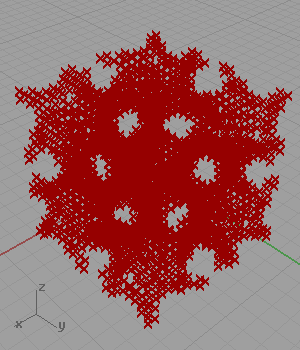
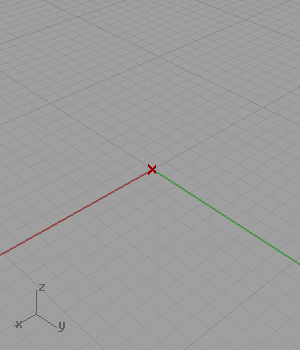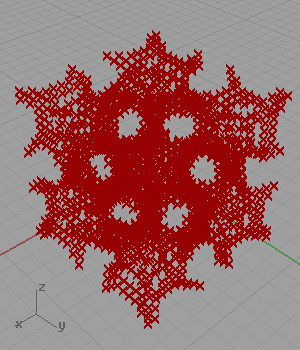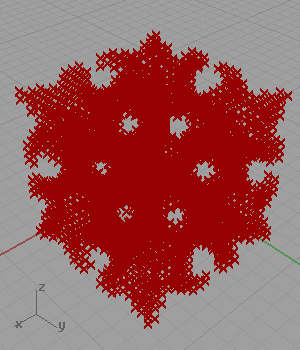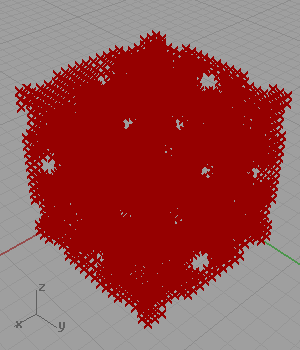
Another famous shape of architectural geometry is a set of definitions creating minimal surfaces. I’ve found the trigonometric equation of the Gyroid and created a simple logic for approximating it as points in Grasshopper. However, when I searched the net for similar solutions, I found lots of them including the same approach as mine (Wynstan Wu’s definition). I was planning to develop a script in Grasshopper to take these estimated points and pull them to the Gyroid surface.
Then, I found that even there are people already done that as separate components in Grasshopper. This means, creating abstract geometric solutions for minimal surfaces is not an advanced problem, in contrast, it has become an introductory problem to be studied in basic education of computational design. As we know, abstract geometrical modeling is only one domain of a design mind. Other domains such as material and fabrication techniques are still to be studied at a more advanced level. This website has a very good explanation of gyroid for dummies like me.
In my code for approximating Gyroid, I generated a three-dimensional grid of points. Then, I checked if the coordinates of any point is close enough to the following equation: cos(x)sin(y)+cos(y)sin(z)+cos(z)*sin(x). However, this 2012 definition is not working anymore. This is because of the fact that the Construct Point component does not create a 3D grid. I added a little randomness and fixed that issue in 2023. Below is the updated definition:
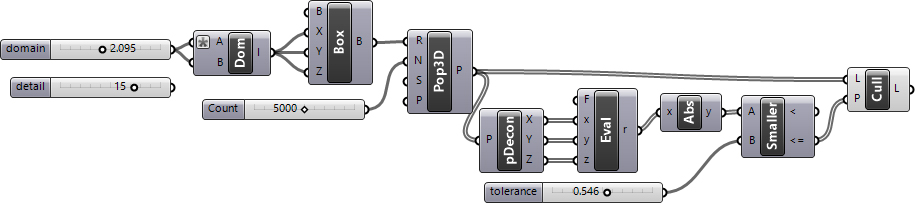
You can re-build the definition by looking at the image above and the explanation. The “*” in the Domain component is “-x”.
Cite this post
Related Posts
Modeling the Gyroid Solid
March 30, 2024
Gyroid is a popular triply-periodic minimal surface. Although it is a mathematical entity, designers and architects like its approximations very much. We used an interpretation of Gyroid in the rammed-earth structure: “Common-action Wall” in 2017. In that project, we utilized its spatial quality of dividing the space into two intertwining and symmetrical volumes. By making one of these volumes solid, I left the other void. So, in this tutorial, I am going to explain modeling the Gyroid Solid by utilizing…
Modeling The Gyroid
May 16, 2023
Here is the method I used for approximately modeling the Gyroid, a triply-periodic minimal surface. It is very popular in architecture because the symmetrical solids and voids it generates are interesting. I modeled this for the Common-action Wall project we exhibited together with Fulya Akipek in 2017. After several attempts to generate it in Grasshopper, I decided to model it in Rhino. There are some sources on the internet, explaining the geometric modeling process. However, none of them was giving…
This is the new paper with Meryem Nurefşan Yabanigül, published at Automation in Construction. It is also Meryem’s master’s thesis. This study is about testing the production of curved surfaces with non-linear robotic hotwire cutting and shape memory alloys. Below is the abstract of it: Robotic arms are being used by construction firms and schools of architecture around the world in design/build research and material studies. Some of these studies utilize robotic hot wire cutting (RHC) as an efficient production…
S-ARCH Award
June 4, 2018
The “Common-Action Wall” Project of the POTplus Design Research Group, founded by Fulya Akipek and Tuğrul Yazar from BİLGİ Faculty of Architecture, got an honorable mention in the category of “Completed Projects/Small Projects” in “S.ARCH 2018 Project Award”. For detailed information about the “Common-Action Walls” Project, please click here and here Members of the Jury: Toyo Ito, Toyo Ito & Associates, Architects (Japan)Prof. Will Alsop, aLL Design (UK)Mats Ove Frosterud, TENGBOM (Sweden)Prof. Leon van Shaik, RMIT University (Australia)Viviana Muscettola, Zaha Hadid Architects (UK)Peter Exley, Architecture is Fun (USA)Jan Mattsson,…
Common-action Wall
January 9, 2018
In 2017, during the 4th International Architecture Biennial of Antalya, we constructed the Common-action Wall in Karaalioğlu Park. We designed this architectural prototype as a wall that enables the growth and harvesting of edible plants for park users. To facilitate plant growth and ensure sunlight access, as well as to direct rainwater toward the plants, we conducted extensive studies on minimal surfaces. Ultimately, we found that the gyroid form met all the requirements. It proved advantageous during the production process,…