Fourier Series

by Tuğrul Yazar | November 14, 2022 14:06

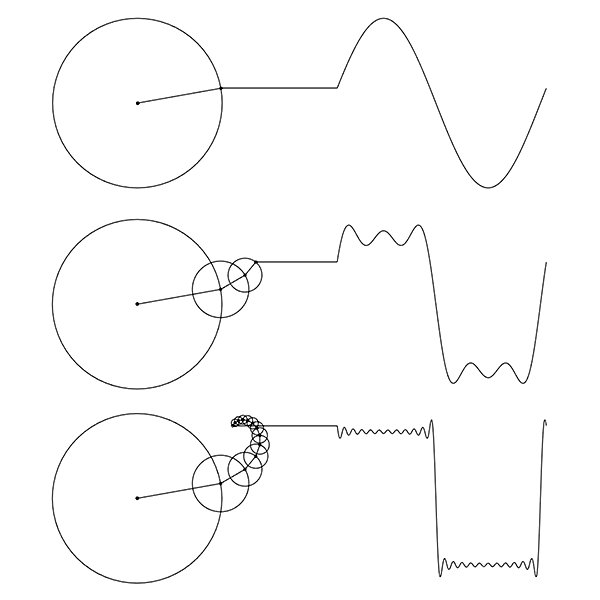
This is my first experiment with the Fourier Series in Grasshopper[1] using Python[2]. This is a technique to decompose functions into their frequency components. Fourier series have a wide range of applications in physics and engineering. What makes it especially fascinating, however, is the visual intuition it offers. It looks like a kind of mathematical “magic” that emerges from the geometry of frequency. I explored several excellent visual explanations online, including those by Coding Train[3], 3Blue1Brown[4], and Mathologer[5], each offering a unique perspective.

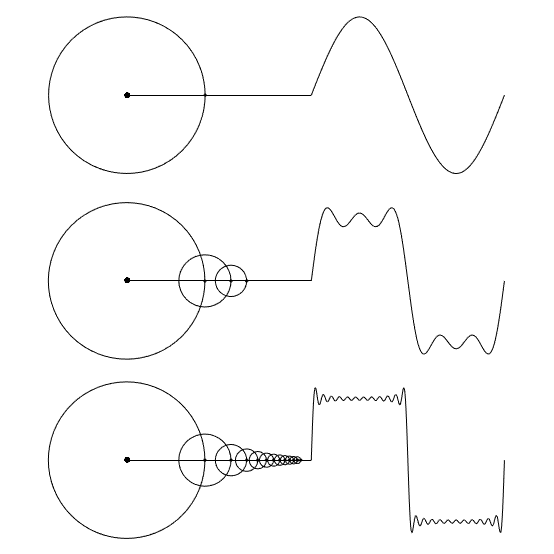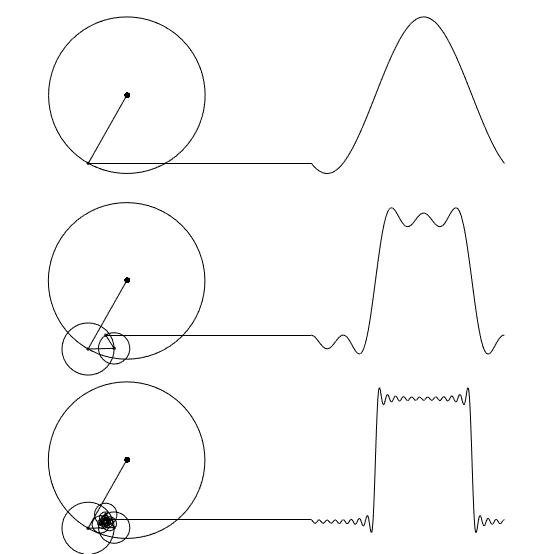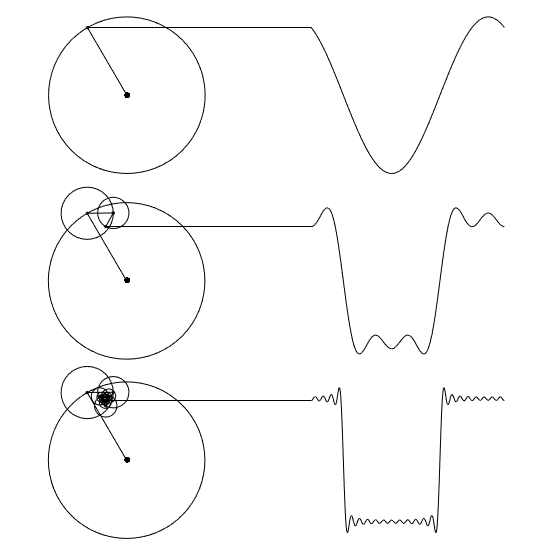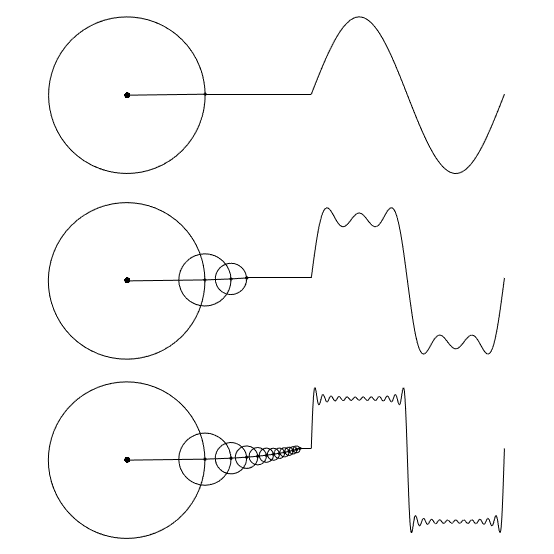
This Grasshopper definition includes a Python component that animates a set of rotating circles and the resulting wave. It serves as an introduction to more complex explorations. The N input controls the number of circles (harmonics), allowing you to observe how increasing complexity affects the wave. The t input advances the rotation, enabling animation. This is an early-stage experiment. I aimed at understanding the fundamentals of the technique. The more intriguing direction would be to reverse the process: given a waveform, the circle parameters that reconstruct it would be determined. This can be the core purpose of the Discrete Fourier Transform. I studied that topic here[6].

import rhinoscriptsyntax as rs
import math
a, b, c, wave_pts = [], [], [], []
dt, t = math.pi / 200, -2 * t * math.pi
x, y = P[0], P[1]
for i in range(N):
    n = i * 2 + 1
    r = 4 / (n * math.pi)
    prev = [x, y, 0]
    x += r * math.cos(n * t)
    y += r * math.sin(n * t)
    a += [rs.AddCircle(prev, r), rs.AddCircle([x, y, 0], 0.02)]
    b.append(rs.AddLine([x, y, 0], prev))
tw = 2 * math.pi
while tw > 0:
    wy = P[1] + sum(4 / ((i * 2 + 1) * math.pi) * math.sin((i * 2 + 1) * (t + tw)) for i in range(N))
    wave_pts.append([3.6 + tw / 2, wy, 0])
    tw -= dt
c.append(rs.AddInterpCurve(wave_pts))
b.append(rs.AddLine([x, y, 0], [3.6, y, 0]))

Above is the Fourier Series code I wrote in the Python[2] component. So, it should work in Rhino 6, 7, and 8 without problems. However, you can rebuild the component by copying the code above. Or, would you consider being my Patreon if you liked this content and want to download the Grasshopper file? Here[7] is the link to my Patreon page, including the working Grasshopper file for the Fourier Series and many more.

Source URL: https://www.designcoding.net/fourier-series/