The story of Atatürk Cultural Center (in Turkish: Atatürk Kültür Merkezi – AKM) dates back to the 1930s. Auguste Perret designed the first version of the project and started the construction in the late ’30s. However, war and financial problems halted the construction. The project…

This group used aluminum expanded mesh in order to test its balance between structural capacity and weight. They folded different-sized sheets to create components, then assembled them creating a span of 2,5 meters approx. They managed to control the macro form by manipulating the component…

The material system of group 2 at İBU Basic Design project was based on a component developed using tensegrity forces on aluminum bands. Although it was hard to maintain structural solidity with the heavy material, they proved that letting aluminum fly over a predefined distance…

The following posts will include some of the final projects, completed in Basic Design Studio, İstanbul Bilgi University Faculty of Architecture in 2013. Below, you see the amazing work of group 1, an interlocking system that presents diversity and structural integrity at the same time….

The exploration of the concept of “patronus – pattern” in architecture is presented in a captivating and insightful manner. This issue of AD, although older, continues to hold relevance in the contemporary realm of architectural design, covering various aspects of the conception and utilization of…

A newly established student club, “E3 Architecture and Design” is organizing a two-day workshop at İstanbul Bilgi University Faculty of Architecture between June 10-11, 2013. The Grasshopper Workshop will be the first one in the faculty. The event will be conducted at our computer lab….

Becoming popular after the Beijing 2008 Olympics National Aquatics Centre‘s facade (which is believed to be a Voronoi subdivision, as an epic mistake), the Weaire Phelan structure is a solution of equal volumes with minimal surface area. This nice website briefly explains the phenomenon. There…

Below is the final production of the three-day workshop at Bolu İzzet Baysal University Faculty of Engineering and Architecture. For more information about the process and the photos from the first student prototypes, you may visit the workshop blog at infections2.blogspot.com Grasshopper definition developed within the…

This is an old research paper, prepared with Birgül Çolakoğlu. It is in Turkish and includes our first results in some of the Rhinoscript exercises. Here is the abstract of the paper; Recent research in architecture have focused on to understand computational methods of formal…

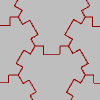
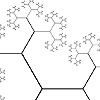
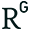The Parquet Deformation exercise is generally originated with William Huff. Huff conducted it at several schools of architecture since the 1960s. Huff defines the exercise as rooted in two analytical disciplines; monohedral tilings in geometry, and the continuous deformations in biological morphology. This is generally…

I’ve seen beautiful examples of similar compositions made using vector field components in Grasshopper. I just tried to make my own animate field lines to see how they float over force dynamics. In essence, these compositions could also be done using regular vector components but…

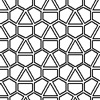
In Design Computing class, we have discussed how the parametric wall study (here) can be implemented to describe regular curved surfaces such as domes. This led us to well-known design compositions named Muqarnas. Previously we have studied how a parametric muqarnas definition could be in…

The “Re_Flex Patterning” workshop will be conducted at İzzet Baysal University Faculty of Engineering and Architecture between 6-8th May 2013. The workshop is led by Tuğrul Yazar and Fulya Akipek, from the İstanbul Bilgi University Faculty of Architecture. Integrating digital media with the material world…

WFC Shangai is a design exercise in our first-year Design Computing class introduced by Onur Yüce Gün. This exercise emphasizes both analytical thinking and associative geometry and aims to utilize boolean operations as solid and void references in creating forms. We asked students to develop…

Here are some student works about the parametric wall exercise I briefly explained here along with a Grasshopper implementation of the core wall definition. Students are expected to design their own brick and compose it in a way that generates a seamless wall surface. Ömer Kirazoğlu…

This is a first-year design computing problem we studied last month. It is a simple parametric wall exercise introduced by Mete Tüneri. Creating a simple definition of a building brick to be placed on a straight path, and then manipulating the path to reform different…

This is a solid-void (or boolean) exercise for first-year students. It is initially introduced by Onur Yüce Gün as an in-class exercise but later became a design problem also. Before getting into the parametric wall and eventually muqarnas exercises, this small but effective assignment helps…

Today’s design computing class was about fractals. In Rhino, writing macro statements are very easy to learn as it just mimics your behaviors in a sequential text. There are a few syntactic rules that we should know. First, you should watch the command line carefully…

One of the cult texts in Shape Grammars theory is Stiny‘s Chinese Ice-ray Lattices Grammars. Although it is full of technical terms, it represents an analysis of a working algorithm. We can directly transfer that from the behavior of an artist. “One can imagine a…

One of the main requirements of being successful in the field of digital design seems to have nice high-tech background images. Usually, it contains different kinds of nebula-like grids, plastic-explicit, and/or combinations of curves-surfaces-and-numbers, burnt by a couple of photoshop filters. If you have the right…